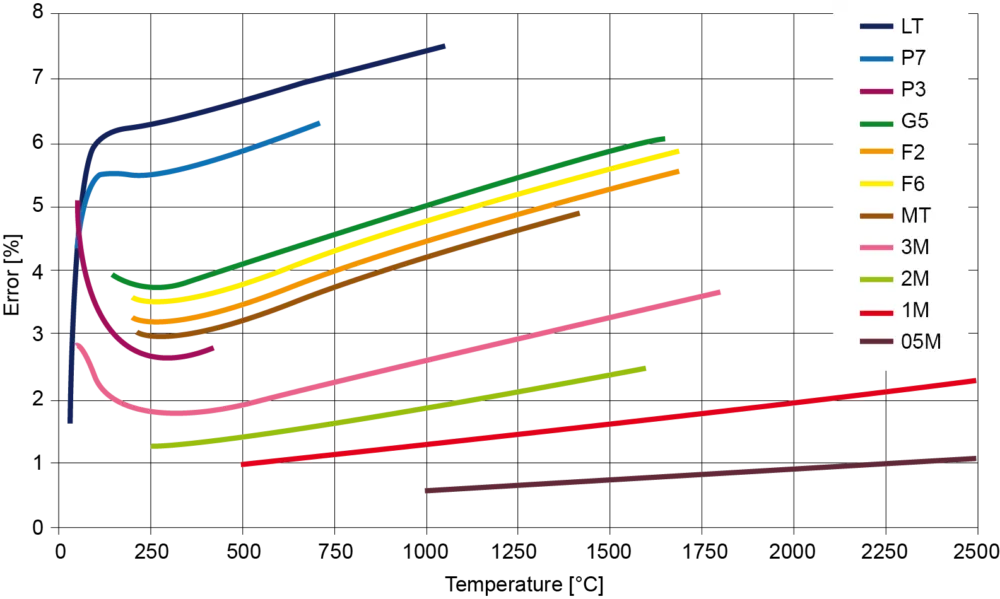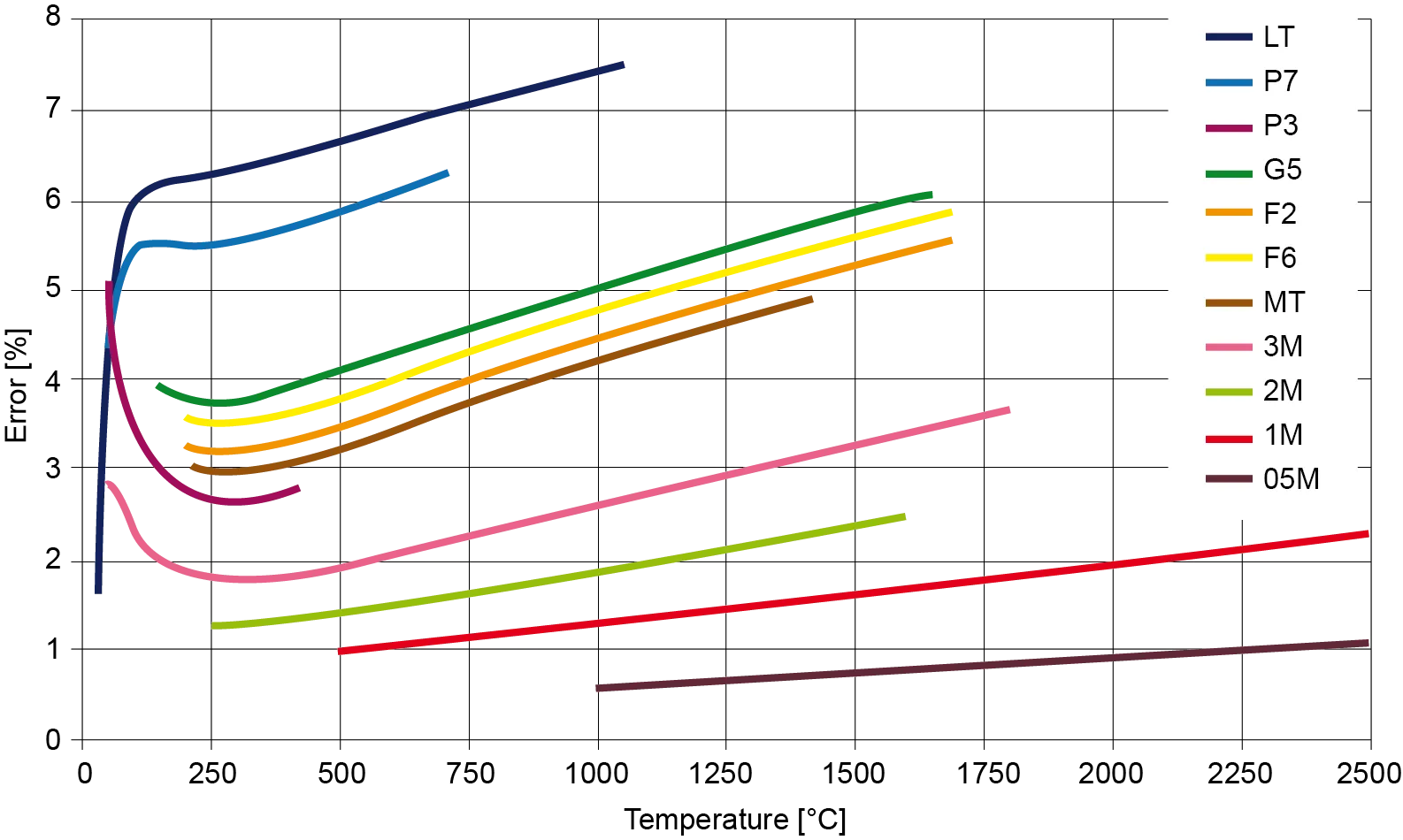Emissivity

The emissivity [math](ε)[/math] measures an object’s ability to emit thermal radiation. It is the ratio of the radiance of a real object to an ideal thermal source, known as a black body. While a black body has an emissivity of 1, all real objects have an emissivity of less than 1.

Emissivity [math]ε = ε(\theta,\phi,\lambda,T)[/math] is a function of the radiation angle [math](\theta,\phi)[/math] relative to the surface, the wavelength [math](\lambda)[/math], and the temperature [math](T)[/math]. Most commercially available infrared thermometers are calibrated against a blackbody radiator. If the emissivity of a measurement object is known and set in the device configuration, the measurement signal can be correlated to the ideal thermal emitter, and its surface temperature can be calculated.

The directional emissivity slowly decreases for non-metallic surfaces as the deviation from the vertical viewing angle increases. For metallic surfaces, the angular dependence is more complex. Depending on the application or material, these influences on the measurement uncertainty may or may not be negligible.

Special spectral filters can be used to limit the angular dependence of emissivity, generating correct measured values for all image areas, especially for cameras with wide aperture angles.

Emissivity can also be considered for a single wavelength for all directions of radiation, known as spectral hemispherical emission, or for all wavelengths, known as total hemispherical emissivity. Hemispherical emissivity for non-metallic materials is relatively high and constant at high wavelengths, while for bare metal surfaces, it is significantly lower and drops at longer wavelengths.

As emissivity is used as a correction factor in the radiation balance calculation, the measurement uncertainty increases as emissivity decreases. It is advisable to use a measuring device with a spectral sensitivity at which the object emissivity is as high as possible [math](ε(\lambda) = ε_{max})[/math]. For metals, this would be the shortest possible wavelengths that still meet the requirements for the measuring temperature range.

The influence of this effect on the measured value can be reduced by setting the emissivity to a value close to the main operating point so that deviations only occur for significantly lower or higher object temperatures. Alternatively, the use of a ratio pyrometer can help reduce the measurement error if the influence of the object temperature on the emissivity is relatively independent of the wavelength [math](ε(\lambda,T) \sim (ε(T))[/math].